6427. Beehives

Bees are one of the most industrious insects. Since they collect nectar and pollen from flowers, they have to rely on the trees in the forest. For simplicity they numbered the n trees from 0 to n – 1. Instead of roaming around all over the forest, they use a particular list of paths. A path is based on two trees, and they can move either way i.e. from one tree to another in straight line. They don’t use paths that are not in their list.

As technology has been improved a lot, they also changed their working strategy. Instead of hovering over all the trees in the forest, they are targeting particular trees, mainly trees with lots of flowers. So, they planned that they will build some new hives in some targeted trees. After that they will only collect their foods from these trees. They will also remove some paths from their list so that they don’t have to go to a tree with no hive in it.

Now, they want to build the hives such that if one of the paths in their new list go down (some birds or animals disturbs them in that path) it’s still possible to go from any hive to another using the existing paths.

They don’t want to choose less than three trees and as hive-building requires a lot of work, they need to keep the number of hives as low as possible. Now you are given the trees with the paths they use, your task is to propose a new bee hive colony for them.

Input. Starts with the number of test cases t (t ≤ 50). Each case starts with a blank line. Next line contains two integers n (2 ≤ n ≤ 500) and m (0 ≤ m ≤ 20000), where n denotes the number of trees and m denotes the number of paths. Each of the next m lines contains two integers u v (0 ≤ u, v < n, u ≠ v) meaning that there is a path between tree u and v. Assume that there can be at most one path between tree u to v, and needless to say that a path will not be given more than once in the input.

Output. For each case, print the case number and the number of beehives in the proposed colony or “impossible” if its impossible to find such a colony.

Sample input	Sample output
3 3 3 0 1 1 2 2 0 2 1 0 1 5 6 0 1 1 2 1 3 2 3 0 4 3 4	Case 1: 3 Case 2: impossible Case 3: 3

SOLUTION

graphs, breadth first search

Algorithm analysis

Find the cycle of minimum length in the graph.

Start the breadth first search from each vertex. For example, let we start bfs(i) (0 ≤ i < n). If during the search we meet an already visited vertex, a cycle is found. Let d[j] stores the length of the shortest path from start i to vertex j. Suppose that when passing along the edge u → v it turns out that v has already been passed (d[v] ≠ INF). This means the presence of a cycle of length d[u] + d[v] + 1.

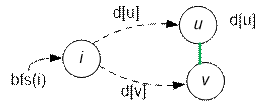
Among all the found cycles, find one with the smallest length.

Example

Graphs given in a sample, have the form:

First and third graphs have a cycle of length 3.

Algorithm realization

Declare a constant infinity INF. Declare an adjacency list of the graph g.

#define INF 2000000000

vector<vector<int> > g;

Function bfs implements a breadth first search from the vertex start. Find the size of the minimum cycle in the variable res.

int bfs(int start)

{

int res = INF;

vector<int> d(n, INF);

vector<int> prev(n, -1);

queue<int> q;

q.push(start);

The value d[v] stores the shortest distance (in terms of the number of edges) from start to v.

d[start] = 0;

while (!q.empty())

{

int u = q.front();

q.pop();

for (int i = 0; i < g[u].size(); i++)

{

int to = g[u][i];

if (to == prev[u]) continue;

If the vertex to is not visited yet (d[to] = INF), then add it to the queue.

if (d[to] == INF)

{

d[to] = d[u] + 1;

prev[to] = u;

q.push(to);

}

The vertex to has already been visited. Cycle is found. There is a path from start to u of length d[u] and from start to to of length d[to]. Just now we found an edge (u, to) that forms a cycle. The cycle length is d[to] + d[u] + 1.

else

{

res = min(res, d[to] + d[u] + 1);

If the cycle length equals to 3, then it can not be decreased more.

if (res == 3) return 3;

}

}

}

return res;

}

The main part of the program. Read the input data.

scanf("%d", &cases);

for (cs = 1; cs <= cases; cs++)

{

scanf("%d %d", &n, &m);

g.clear();

g.resize(n);

Read the edges of the graph, build an adjacency list.

for (int i = 0; i < m; i++)

{

int u, v;

scanf("%d %d", &u, &v);

g[u].push_back(v);

g[v].push_back(u);

}

Run the breadth first search from each vertex i. Store the length of minimum cycle in the variable res.

int res = INF;

for (i = 0; i < n; i++)

{

res = min(res, bfs(i));

if (res == 3) break;

}

Print the answer. If res = INF, then there is no cycle in the graph.

printf("Case %d: ", cs);

if (res == INF) puts("impossible");

else printf("%d\n", res);

}

Java realization

import java.util.*;

public class Main

{

static ArrayList<Integer>[] g;

static int dist[], prev[];

static int bfs(int start)

{

int res = Integer.MAX_VALUE;

Arrays.fill(dist,-1);

dist[start] = 0;

Arrays.fill(prev,-1);

Queue<Integer> q = new LinkedList<Integer>();

q.add(start);

while(!q.isEmpty())

{

int v = q.poll();

for(int i = 0; i < g[v].size(); i++)

{

int to = g[v].get(i);

if (to == prev[v]) continue;

if (dist[to] == -1)

{

q.add(to);

prev[to] = v;

dist[to] = dist[v] + 1;

}

else

{

res = Math.min(res, dist[to] + dist[v] + 1);

if (res == 3) return 3;

}

}

}

return res;

}

@SuppressWarnings("unchecked")

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int cases = con.nextInt();

for (int cs = 1; cs <= cases; cs++)

{

int n = con.nextInt();

int m = con.nextInt();

g = new ArrayList[n];

for(int i = 0; i < n; i++)

g[i] = new ArrayList<Integer>();

dist = new int[n];

prev = new int[n];

for (int i = 0; i < m; i++)

{

int u = con.nextInt();

int v = con.nextInt();

g[u].add(v);

g[v].add(u);

}

int res = Integer.MAX_VALUE;

for (int i = 0; i < n; i++)

{

res = Math.min(res, bfs(i));

if (res == 3) break;

}

System.out.print("Case " + cs + ": ");

if (res == Integer.MAX_VALUE) System.out.println("impossible");

else System.out.println(res);

}

con.close();

}

}